Priorización de zonas mediante modelo SIG Ponderativo

Priorización de zonas mediante modelo SIG Ponderativo

Modelo METRIC

Mapping Evapotranspiration with Internalized Calibration

Modelo Hidrológico de Schaake

Modelo de Balance Hídrico Mensual Schaake en la Cuenca hidrográfica de Lurín

Schaake Monthly Water Balance Model in the Lurin Drainage Basin

Por Eber Risco Sence

Los profesionales de las ciencias ambientales deben afrontar la escasez de datos hidrológicos para desarrollar su trabajo dentro de los distintos ámbitos que les toque desempeñar. Para ello se ven forzados al empleo de metodologías de simulación hidrológica, la cual se puede definir como la descripción matemática de la respuesta de un sistema hidrológico a una serie de eventos programados durante un periodo de tiempo.

1.       Área de estudio y datos

La cuenca hidrográfica de Lurín, políticamente se encuentra ubicada en la región Lima, dentro de las provincias de Lima y Huarochirí. La cuenca hidrográfica del río Lurín analizada en la presente investigación tiene una extensión aproximada de 1451.24 km2, desde la partición de aguas hasta la estación Puente Manchay. Geográficamente la cuenca del río Lurín está comprendida entre las coordenadas (UTM-Zona 18S) Este: 297644-367577 y Norte: 8650619-8690883.

Figura 1: Ubicación de las estaciones meteorológicas de la cuenca del río Lurín.

Las estaciones pluviométricas utilizadas fueron: Manchay, Antioquia, Matucana, Langa, Tuna, Huarochiri, Escomarca, Parac, Chalilla; y las estaciones hidrométricas de Antapucro y Puente Manchay.

2.       Metodología

2.1   Modelo Schaake

Schaake y Liu (1989) desarrollaron un modelo de balance hídrico simple para la evaluación del impacto del cambio climático. Schaake (1990) mejoro el algoritmo de agua subterránea del modelo lineal usando un reservorio no lineal. El modelo mejorado tiene la capacidad de simular la escorrentía sobre un rango de condiciones climáticas. Este modelo introduce el déficit de humedad del suelo en la expresión de la escorrentía y evapotranspiración. La escorrentía total está dividida en escorrentía superficial y flujo subterráneo.

 Figura 2: Esquema del modelo hidrológico conceptual de Schaake.

3.       Resultados

Se ha seleccionado el periodo de enero 1964 a diciembre 1993 para la calibración y de enero 1994 a diciembre 2002 para la validación.  Con el fin de utilizar los criterios de optimización se eligió la función objetiva de Nash y Sutcliffe (1970).

Donde:

Q_si= caudal simulado (m3/s).

Q_ob= caudal observado (m3/s).

N= representa el número de pasos de tiempo simulados.

Para evaluar la bondad de los resultados del modelo durante los periodos de calibración y validación, los intervalos se presentan el Cuadro 1. La eficiencia de Nash se encuentra enmarcada como C3.

 

 Cuadro 1: Criterios para evaluar el desempeño de los modelos en categorías desde excelente a muy mala. FUENTE: Andersen et al, citados por Miroslaw y Okruszko 2011

3.1   Optimización del modelo Schaake

La optimización del modelo fue realizada mediante técnicas de optimización global, donde un mínimo global es un punto donde el valor de la función es menor que o igual al valor en todos los otros puntos factibles.

Los valores obtenidos para los parámetros del modelo Schaake fueron: Máximo déficit de humedad en el reservorio del suelo D_max=184.7435; parámetro que representa la proporción de la actual evapotranspiración que debe ser satisfecha por la precipitación en el mes actual antes de la escorrentía o la infiltración que puede ocurrir Φ=0.3497; el parámetro que controla la infiltración de la precipitación a través de la superficie del suelo z=0.0001; el parámetro del modelo kk=0.1886; el valor umbral máximo para el modelo G_max=184.9065. En la figura 3 se muestra el comportamiento de los parámetros en el proceso de optimización, en la figura 4 se muestra las variaciones de los parámetros tomados de dos en dos de acuerdo al valor de Nash-Sutcliffe obtenido.

 Figura 3: Comportamiento de los parámetros D_max, Φ ,z, kk, G_max en el proceso de optimización global, donde la variación va desde el azul al rojo, siendo el rojo los valores más adecuados para el modelo de acuerdo a la función objetivo seleccionada.

 Figura 4:Variación de la eficiencia de la función Nash-Sutcliffe de acuerdo a la variación de los parámetros D_max, Φ ,z, kk, G_max , superficies generadas tomando de dos en dos los parámetros.

3.2   Calibración del modelo Schaake

En el periodo de calibración (1964-1993) el modelo Schaake presentó una eficiencia de Nash-Sutcliffe de  90.95 % considerado como una calidad excelente de acuerdo a la tabla 1. En la figura 5 se muestra los caudales simulados comparados con los observados.

 Figura 5: Caudales observados y simulados por el modelo Schaake en la cuenca del río Lurín

(Periodo de calibración)

3.3   Validación del modelo Schaake

En el periodo de validación (1994-2002) el modelo Schaake presentó una eficiencia de Nash-Sutcliffe de  93.04 % considerado como una calidad excelente de acuerdo a la tabla 1. En la figura 6 se muestra los caudales simulados comparados con los observados.

 Figura 6:Caudales observados y simulados por el modelo Schaake en la cuenca del río Lurín

(Periodo de validación).

4.       Conclusión

• De acuerdo a los resultados obtenidos, el modelo Schaake se presenta como adecuado para la simulación hidrológica en la cuenca del río Lurín, presenta una eficiencia de 90.95 % y 93.04 % para los periodos de calibración y validación respectivamente.

5.       Referencias bibliográficas

1. Fernandez, R; Vogel, S. 2000. Regional calibration of watershed model. Hydrological Sciences-journal-des-Sciences Hydrologiques, 45(5): 689-707.
2. Jiang, T; Xu, C. 2007. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. Journal of Hydrology 336: 316-333.
3. Miroslaw, D; Okruszko, T. 2011. Modelling of Hydrological Processes in the Narew Catchment. New York, US.Springer. 153 p.
4. Schaake, J.C., 1990. From climate to flow. In: Waggoner, P.E. (Ed.), Climate change and US Water Resources. John Wiley & Sons, New York, pp. 177–206.
5. Schaake, J.C., Liu, L.Z., 1989. Development and application of simple water balance models to understand the relationship between climate and water resources. In: Kavvas, M.L. (Ed.), New Directions for Surface Water Modelling (Proceedings of the Baltimore Symposium, May 1989). IAHS Publication, No.181, pp. 345–352.

Aplicación en MATLAB

Modelo Hidrológico Thornthwaithe-Mather

Modelo de Balance Hídrico Mensual Thornthwaithe-Mather en la Cuenca hidrográfica de Huancané

Thornthwaithe-Mather Monthly Water Balance Model in the Huancane Drainage Basin

Por Eber Risco Sence

Para una evaluación de los recursos hídricos a una escala regional, los modelos de balance hídrico mensual son muy utilizados para la identificación de las consecuencias hidrológicas por cambios en la temperatura, precipitación y otras variables climáticas.

1.       Área de estudio y datos

La cuenca hidrográfica de Huancané, políticamente se encuentra ubicada en la región Puno, dentro de las provincias de Azángaro, San Antonio de Putina, Huancané y Moho. La cuenca hidrográfica del río Huancané analizada en la presente investigación tiene una extensión aproximada de 3633.92 km2, desde la partición de aguas hasta la estación Puente Huancané. Geográficamente la cuenca del río Huancané está comprendida entre las coordenadas (UTM-Zona 19S) Este: 376198-468591 y Norte: 8302030-8397464.

  Figura 1: Ubicación de las estaciones meteorológicas de la cuenca del río Huancané.

Las estaciones pluviométricas utilizadas fueron: Estaciones pluviométricas para la cuenca del río Huancané: Taraco, Arapa, Huancané, Huaraya, Progreso, Muñani, Putina, Azángaro, Ananea, Crucero, Cojata y la estación hidrométrica de Puente Huancané.

2.       Metodología

2.1   Modelo Thornthwaithe-Mather

El modelo fue desarrollado por Thornthwaithe y Mather (1955), es un modelo de doble reservorio (ver figura 2). El modelo tiene dos parámetros a ser calibrados: capacidad de humedad del suelo y el almacenamiento constante.

 

  Figura 2: Esquema del modelo hidrológico conceptual Thornthwaithe-Mather.

3.       Resultados

Se ha seleccionado el periodo de enero 1964 a diciembre 1993 para la calibración y de enero 1994 a diciembre 2002 para la validación.  Con el fin de utilizar los criterios de optimización se eligió la función objetiva de Nash y Sutcliffe (1970).

Donde:

Q_si= caudal simulado (m3/s).

Q_ob= caudal observado (m3/s).

N= representa el número de pasos de tiempo simulados.

Para evaluar la bondad de los resultados del modelo durante los periodos de calibración y validación, los intervalos se presentan el Cuadro 1. La eficiencia de Nash se encuentra enmarcada como C3.

 

 Cuadro 1: Criterios para evaluar el desempeño de los modelos en categorías desde excelente a muy mala. FUENTE: Andersen et al, citados por Miroslaw y Okruszko 2011.

3.1   Optimización del modelo Thornthwaithe-Mather

El proceso de optimización del modelo fue realizada mediante técnicas de optimización global, para lo cual se utilizó un algoritmo genético. Los algoritmos genéticos son métodos adaptativos, muy utilizados en problemas de búsqueda y optimización de parámetros, basados en la mecánica de selección natural y de la genética natural. Combinan la supervivencia del más apto entre estructuras de secuencias con un intercambio de información estructurado, aunque aleatorio, para constituir así un algoritmo de búsqueda que tenga algo de genialidades de las búsquedas humanas (Goldberg, 1989).

  

Figura 3: Diagrama de flujo de los algoritmos genéticos. FUENTE: Haupt y Haupt (2004).

Los valores obtenidos para los parámetros del modelo fueron: ϕ= 25.2109, λ =    0.5643. En la figura 4 se muestra el proceso de optimización con algoritmo genético de manera gráfica y en la figura 5 se muestra el comportamiento de los parámetros en el proceso de optimización y las variaciones de los parámetros de acuerdo al valor de Nash-Sutcliffe obtenido.

 Figura 4: Gráficos del proceso de optimización mediante algoritmo genético en el modelo de balance hídrico Thornthwaithe-Mather.

Figura 5: Variación de la eficiencia de la función Nash-Sutcliffe de acuerdo a la variación de los parámetros ϕ, λ .Superficies generadas tomando de dos en dos los parámetros.

3.2   Calibración del modelo Thornthwaithe-Mather

En el periodo de calibración (1964-1993) el modelo Thornthwaithe-Mather presentó una eficiencia de Nash-Sutcliffe de  73.15 % considerado como una calidad muy buena de acuerdo a la tabla 1. En la figura 6 se muestra los caudales simulados comparados con los observados.

Figura 6: Caudales observados y simulados por el modelo Thornthwaithe-Mather en la cuenca del río Huancané (Periodo de calibración)

3.3   Validación del modelo Thornthwaithe-Mather

En el periodo de validación (1994-2002) el modelo Thornthwaithe-Mather presentó una eficiencia de Nash-Sutcliffe de 81.95 % considerado como una calidad muy buena de acuerdo a la tabla 1. En la figura 7 se muestra los caudales simulados comparados con los observados.

Figura 7: Caudales observados y simulados por el modelo Thornthwaithe-Mather en la cuenca del río Huancané (Periodo de validación)

4.       Conclusión

• De acuerdo a los resultados obtenidos, el modelo Thornthwaithe-Mather se presenta como adecuado para la simulación hidrológica en la cuenca del río Huancané, presentando una eficiencia de 73.15 % y 81.95 % para los periodos de calibración y validación respectivamente.

5.       Referencias bibliográficas

1. Fernandez, R; Vogel, S. 2000. Regional calibration of watershed model. Hydrological Sciences-journal-des-Sciences Hydrologiques, 45(5): 689-707.
2. Goldberg, D. 1989. Genetic Algorithms in Search, Optimization and Machine Learning: Addison-Wesley Longman Publishing Co., Inc., Boston, MA, US.
3. Haupt, R; Haupt, S. 2004. Practical Genetic Algorithms. New York, Jhon Wiley & SONS. 261 p.
4.  Jiang, T; Xu, C. 2007. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. Journal of Hydrology 336: 316-333.
5. Miroslaw, D; Okruszko, T. 2011. Modelling of Hydrological Processes in the Narew Catchment. New York, US.Springer. 153 p.
6. Pizarro, R; Soto, M. 2005. Aplicación de dos Modelos de Simulación Integral Hidrológica, para la estimación de caudales medios mensuales, en dos cuencas de Chile central. BOSQUE 26(2):123-129.
7. Thornthwaite, C.W., Mather, J.R., 1955. The Water Balance. Publications in Climatology, vol. 8. Laboratory of Climatology, Drexel Institute of Technology, Centerton, New Jersey. 1–104.

Video de Aplicación en MATLAB

Modelo Hidrológico ABCD

Modelo de Balance Hídrico Mensual ABCD en la Cuenca hidrográfica de Lurín

ABCD Monthly Water Balance Model in the Lurin Drainage Basin

Por Eber Risco Sence

Los profesionales de las ciencias ambientales deben afrontar la escasez de datos hidrológicos para desarrollar su trabajo dentro de los distintos ámbitos que les toque desempeñar. Para ello se ven forzados al empleo de metodologías de simulación hidrológica, la cual se puede definir como la descripción matemática de la respuesta de un sistema hidrológico a una serie de eventos programados durante un periodo de tiempo. El uso más frecuente de la simulación hidrológica es la síntesis de hidrogramas a partir de los datos de precipitación y las características de la cuenca de drenaje, ya sea en una escala temporal pequeña (estudio de eventos) o grande (estudio de recursos).

1.       Área de estudio y datos

La cuenca hidrográfica de Lurín, políticamente se encuentra ubicada en la región Lima, dentro de las provincias de Lima y Huarochirí. La cuenca hidrográfica del río Lurín analizada en la presente investigación tiene una extensión aproximada de 1451.24 km2, desde la partición de aguas hasta la estación Puente Manchay. Geográficamente la cuenca del río Lurín está comprendida entre las coordenadas (UTM-Zona 18S) Este: 297644-367577 y Norte: 8650619-8690883.

   Figura 1: Ubicación de las estaciones meteorológicas en la cuenca del río Lurín.

Las estaciones pluviométricas utilizadas fueron: Manchay, Antioquia, Matucana, Langa, Tuna, Huarochiri, Escomarca, Parac, Chalilla; y las estaciones hidrométricas de Antapucro y Puente Manchay.

2.       Metodología

2.1   Modelo ABCD

El  modelo ABCD es un modelo de cuenca no lineal que acepta la precipitación y evapotranspiración potencial como entradas, produciendo caudales como salida del modelo. Internamente, el modelo también representa el almacenamiento de humedad en el suelo, almacenamiento de agua subterránea, la escorrentía directa, aporte de las aguas subterráneas hacia el cauce, la evapotranspiración actual. Fue originalmente introducido por Thomas (1981) y Thomas et al. (1983).

 

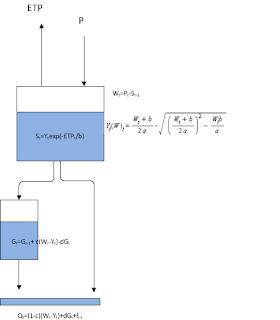
   Figura 2: Esquema del modelo hidrológico conceptual ABCD con los parámetros a, b, c y d a optimizar.

3.       Resultados

Se ha seleccionado el periodo de enero 1964 a diciembre 1988 para la calibración y de enero 1989 a diciembre 2002 para la validación.  Con el fin de utilizar los criterios de optimización se eligió la función objetiva de Nash y Sutcliffe (1970).

Donde:

Q_si= caudal simulado (m3/s).

Q_ob= caudal observado (m3/s).

N= representa el número de pasos de tiempo simulados.

Para evaluar la bondad de los resultados del modelo durante los periodos de calibración y validación, los intervalos se presentan el Cuadro 1. La eficiencia de Nash se encuentra enmarcada como C3.

 

 

 Cuadro 1: Criterios para evaluar el desempeño de los modelos en categorías desde excelente a muy mala. FUENTE: Andersen et al, citados por Miroslaw y Okruszko 2011

3.1   Optimización del modelo ABCD

La optimización del modelo fue realizada mediante técnicas de optimización global, donde un mínimo global es un punto donde el valor de la función es menor que o igual al valor en todos los otros puntos factibles.

Los valores obtenidos para los parámetros del modelo fueron: a=0.2612, b= 69.9574, c= 0.8649 y d=0.9992. En la figura 3 se muestra el comportamiento de los parámetros en el proceso de optimización, en la figura 4 se muestra las variaciones de los parámetros tomados de dos en dos de acuerdo al valor de Nash-Sutcliffe obtenido.

Figura 3 : Comportamiento de los parámetros a, b, c y d en el proceso de optimización global, donde la variación va desde el azul al rojo, siendo el rojo los valores más adecuados para el modelo de acuerdo a la función objetivo seleccionada.

Figura 4: Variación de la eficiencia de la función Nash-Sutcliffe de acuerdo a la variación de los parámetros a, b, c y d, superficies generadas tomando de dos en dos los parámetros.

3.2   Calibración del modelo ABCD

En el periodo de calibración (1964-1988) el modelo ABCD presentó una eficiencia de Nash-Sutcliffe de  91.013 % considerado como una calidad excelente de acuerdo a la tabla 1. En la figura 5 se muestra los caudales simulados comparados con los observados.

Figura 5: Caudales observados y simulados por el modelo ABCD en la cuenca del río Lurín

(Periodo de calibración)

3.3   Validación del modelo ABCD

En el periodo de validación (1989-2002) el modelo ABCD presentó una eficiencia de Nash-Sutcliffe de  94.44 % considerado como una calidad excelente de acuerdo a la tabla 1. En la figura 6 se muestra los caudales simulados comparados con los observados.

Figura 6: Caudales observados y simulados por el modelo ABCD en la cuenca del río Lurín

(Periodo de validación)

4.       Conclusión

• De acuerdo a los resultados obtenidos, el modelo ABCD se presenta como adecuado para la simulación hidrológica en la cuenca del río Lurín, presenta una eficiencia de 91.013 % y 94.44 % para los periodos de calibración y validación respectivamente.

5.       Referencias bibliográficas

1.  Fernandez, R; Vogel, S. 2000. Regional calibration of watershed model. Hydrological Sciences-journal-des-Sciences Hydrologiques, 45(5): 689-707.
2.  Miroslaw, D; Okruszko, T. 2011. Modelling of Hydrological Processes in the Narew Catchment. New York, US.Springer. 153 p.
3. Thomas, H. A. 1981. Improved methods for national water assessment. Report, Contract WR 15249270, US Water Resources Council, Washington, DC, USA.
4. Thomas, H. A., Marin, C. M., Brown1 M. J. & Fierin$, M. B. 1983. Methodolo~ for water r.es.ourcea ssessmentR. Eport NTIS 84-124163, to US GeologIcal Survey, National. Tech. Info. Serv., Spnngfield, VlrgIma, USA.

Aplicación desarrollada en MATLAB

Índice Linealizado de Sombra-Agua

Índice Linealizado de Sombra-Agua

Linearized Shadow and Water Index (SWI) 

Por Eber Risco Sence

       El índice de sombra-agua SWI es útil para detectar lagos. No existen trabajos centrados en la detección de agua en las imágenes de satélite. Sin embargo, las opciones más cercanas en la literatura se basan en la identificación de sombras, las cuales presentan características fotométricas similares al agua.

       En el espectro de IKONOS, el agua muestra una curva de respuesta cada vez mayor hasta la banda azul, que llega al máximo en esta región y luego disminuye monótonamente con el infrarrojo cercano. Así, una representatividad del índice sombra-agua debe estar compuesta de altos valores de azul primero. Idealmente, también debería considerar las bandas verde y roja, pero la banda verde también responde fuertemente a la vegetación y esto dificulta la observación de sombra o agua. Por lo tanto, el índice debe incluir las bandas azul y rojo por lo menos Ünsalan y Boyer (2011).

       Para obtener este índice, se aplicó el mismo esquema utilizado en el NDVI mediante análisis de componentes principales con el azul, rojo, y el infrarrojo cercano. Tratando de maximizar coeficientes banda azul y rojo se obtiene el mejor rendimiento del índice sombra-agua para cada dimensión.

       En un espacio de dos dimensiones, dado que tenemos la intención de tener la banda azul en un SWI, reemplazamos la banda roja con la azul en la formulación NDVI. Obtenemos nuestro primer índice como:

       Para los espacios de tres y cuatro dimensiones, se observa que el tercer componente principal tiene la información sombra en todos los espacios transformados. Los correspondientes índices de agua sombra-γ2, γ3 y γ4 obtenidos a partir de los espacios de transformación están dados de la siguiente manera:

       Con la finalidad de identificar lagunas en la cuenca del río Ocoña, ubicado en el departamento de Arequipa, Perú, a partir de una imagen LANDSAT 5 TM tomada el 16 de agosto de 2008, se procedió a desarrollar la metodología propuesta por Ünsalan y Boyer (2011).

       Los índices de vegetación lineal γ sobre la base de la actividad vegetal, seguido de tres nuevos índices de vegetación: γ2 y γ3 definidos en espacios 3D, y γ4 en el espacio 4D para l la cuenca del río Ocoña se aprecian a continuación.

       Se aprecia que los índices γ1, γ2  y γ4 identifican de buena manera la laguna ubicada en la parte noroeste de la cuenca, mientras el índice  γ3 presenta resultados menos satisfactorios para identificar cuerpos de agua.

Referencias

• Schowengerdt, R. 2007. Remote Sensing-Models and Methods for Image Processing. 3 ed. California, US, Academic Press. 558 p.
• Steven M. de Jong; Freek D. Van der Meer. 2004. Remote Sensing Image Analysis. California, US, Springer. 370 p.
• Schott, J. 2007. Remote Sensing: The Image Chain Approach. 2ed. New York, US. Oxford University Press. 701 p.
• Ünsalan, C.; Boyer, K. 2011. Multispectral Satellite Image Understanding. New York, US. Springer. 203 p.

Detección de Valores Atípicos

Detección de Valores Atípicos

Outlier Detection

Por Eber Risco Sence

Los eventos extremos pueden crear problemas en el análisis y modelización de datos. Por ejemplo, un valor extremadamente grande puede causar en la muestra que la media y la desviación estándar sean mucho mayor que los valores de la población. En el análisis bivariado (es decir, X vs Y), un punto extremo puede influir adversamente en el valor de la muestra de un coeficiente de correlación, además pueden distorsionar los coeficientes de la recta de regresión, lo que sugiere un efecto que puede no reflejar la verdadera relación entre el dos variables (McCuen, 2003).

Después de haber decidido subjetivamente que uno o más valores en una muestra son los eventos extremos, los valores deben ser evaluados objetivamente. La intención es evaluar si el evento extremo es probable que haya ocurrido, si la muestra se obtuvo a partir de la población asumida correctamente. La teoría estadística en forma de una prueba de hipótesis se puede utilizar para tomar una decisión. Si la prueba estadística indica que el evento extremo observado es improbable que haya ocurrido durante el muestreo de la población, el evento extremo se llama atípico (outlier). Un valor atípico es un valor medido que, de acuerdo con una prueba estadística, es poco probable que haya ocurrido de acuerdo al resto de los datos de la muestra.

Después de haber decidido que un evento extremo es un outlier, surge la pregunta: ¿Qué se puede hacer con el valor? Si el valor se mantiene en la muestra, entonces puede distorsionar los valores o relaciones calculadas a partir de la muestra. La eliminación del valor debería producir estadísticas más precisas y relaciones con otras variables. Sin embargo, algunos profesionales se oponen a la eliminación de los outliers. Su argumento es que si el valor fue medido, podría haber ocurrido y no es correcto que sea eliminado de la muestra. Ambos son argumentos legítimos.

Mientras numerosos métodos han sido propuestos, los métodos de Dixon-Thompson y Rosner son utilizados comúnmente. El método de Chauvenet, una tercera prueba para los valores atípicos, es sencilla de implementar y de aplicar. Estos métodos definen un estadístico de prueba como la razón de dos desviaciones y se asume que los datos representan una población normal. El método de Rosner sólo es válido para muestras de más de 25 años. La prueba de Dixon-Thompson se puede aplicar para muestras más pequeñas. El método de Chauvenet se puede utilizar con cualquier tamaño de la muestra. Otros métodos para la utilización están basados en la distribución log-Pearson tipo III. El factor de discriminación más importante es probablemente la distribución supuesta de la población. Algunas pruebas de valores atípicos supone que los datos de la muestra proceden de una distribución de probabilidad normal, mientras que otros son válidos para la distribución Pearson tipo III. La distribución es un factor importante en la selección de la prueba más apropiada. Una decisión basada en una prueba puede no ser válido si los datos se muestrean a partir de una distribución que no es el mismo como se supone en el desarrollo de los valores críticos de la prueba. Dicha aplicación puede identificar valores atípicos más o menos que realmente existen en los datos incluidos en la muestra cuando la asunción de la distribución de la población es incorrecta.

En datos hidrológicos a menudo se supone que presentan una distribución log-normal o log-Pearson tipo III.

Método de Chauvenet

Este método requiere el calculo de la media (µ) y la desviación estándar (σ) de los datos analizados. Entonces el valor más extremo en la muestra, X_o es identificado y utilizado para calcular la desviación normal estándar (Z).

Si el valor calculado excede el valor crítico entonces X_o es considerado outlier.

1964	1965	1966	1967	1968	1969	1970	1971	1972	1973
14.96	46.58	12.12	16.28	4.1	28.97	47.36	47.7	135.7	19.5
1974	1975	1976	1977	1978	1979	1980	1981	1982	1983
19.9	49.3	22.3	17.9	13.2	15.6	3.7	26.5	23.3	213.1
1984	1985	1986	1987	1988	1989	1990	1991	1992	1993
8.9	0.5	12.3	23.2	10.4	39	16.1	17.5	25.9	36.5
1994	1995	1996	1997	1998	1999	2000	2001	2002	2003
34.6	14.2	19.4	63.5	342.3	67.8	34.2	50.2	37.7	13.1

 Tabla 1: Precipitación anual (mm) estación Talla.

De acuerdo a los datos de la tabla 1 la media es 41.13, la desviación estándar es 61.57, el valor extremo es 342.3. Por lo tanto el valor de Z calculado es 4.8913, para una muestra de 40 la probabilidad usada es de 1/80=0.0125, Para un test en dos direcciones con una mitad de probabilidad en cada cola (two tailed) el valor crítico es +-2.4977, por lo tanto el valor 342.3 es considerado outlier.

Método Log-Pearson tipo III (Bulletin 17B)

Bulletin 17B (Interagency Advisory Committee on Water Data, 1982) presenta criterios basados en una prueba unilateral para detectar valores atípicos con un 10% de nivel de significancia.  El valor atípico más alto y bajo son calculados con las siguientes ecuaciones:

Donde Y_L es el límite del logaritmo del valor atípico más alto o bajo, ý es la media del logaritmo de los datos analizados, S_y es la desviación estándar de los valores logarítmicos y K_N es la desviación crítica dada en el Bulletin 17B.

De acuerdo a los datos de la tabla 1 la media logarítmica es 1.3699, la desviación estándar logarítmica es 0.4738, el valor de K_N para 40 datos es 2.682. Por lo tanto 2.6408 y 0.0989 representan los límites máximo y mínimo respectivamente, aplicando antilogaritmo se obtiene como límite máximo 437.3938 mm y límite mínimo 1.2559 mm.

 Figura 1: Límites máximo y mínimo según el método de Log-Pearson tipo III.

De acuerdo a los límites y gráfico 1 se puede apreciar que existe un outilier (año 1985 con 0.5 mm).

Referencias:

• Chandler, R; Scott, M. 2011. Statistical Methods for Trend Detection and Analysis. London, UK, Wiley. 370 p.
• McCuen, R. 2003.Modeling Hydrologic Change.New York, US, CRC Press Company .450 p.
• Reiss, R; Thomas, M. 2007. Statistical Analysis of Extreme Values with Applications to Insurance, Finance, Hydrology and Other Fields. 3 ed. Berlin, DE, Springer Science+Busines Media. 516 p.

Vídeo de Aplicación en MATLAB