Modelo
de Balance Hídrico Mensual Schaake en la Cuenca hidrográfica de Lurín
Schaake Monthly Water
Balance Model in the Lurin Drainage Basin
Por
Eber Risco Sence
Los profesionales de
las ciencias ambientales deben afrontar la escasez de datos hidrológicos para
desarrollar su trabajo dentro de los distintos ámbitos que les toque
desempeñar. Para ello se ven forzados al empleo de metodologías de simulación
hidrológica, la cual se puede definir como la descripción matemática de la
respuesta de un sistema hidrológico a una serie de eventos programados durante
un periodo de tiempo.
1.
Área
de estudio y datos
La cuenca
hidrográfica de Lurín, políticamente se encuentra ubicada en la región Lima,
dentro de las provincias de Lima y Huarochirí. La cuenca hidrográfica del río
Lurín analizada en la presente investigación tiene una extensión aproximada de
1451.24 km2, desde la partición de aguas hasta la estación Puente Manchay.
Geográficamente la cuenca del río Lurín está comprendida entre las coordenadas
(UTM-Zona 18S) Este: 297644-367577 y Norte: 8650619-8690883.
Figura 1: Ubicación de las estaciones meteorológicas de la cuenca del río Lurín.
Las estaciones
pluviométricas utilizadas fueron: Manchay, Antioquia, Matucana, Langa, Tuna,
Huarochiri, Escomarca, Parac, Chalilla; y las estaciones hidrométricas de Antapucro
y Puente Manchay.
2.
Metodología
2.1
Modelo
Schaake
Schaake y Liu (1989)
desarrollaron un modelo de balance hídrico simple para la evaluación del
impacto del cambio climático. Schaake (1990) mejoro el algoritmo de agua
subterránea del modelo lineal usando un reservorio no lineal. El modelo
mejorado tiene la capacidad de simular la escorrentía sobre un rango de
condiciones climáticas. Este modelo introduce el déficit de humedad del suelo
en la expresión de la escorrentía y evapotranspiración. La escorrentía total
está dividida en escorrentía superficial y flujo subterráneo.
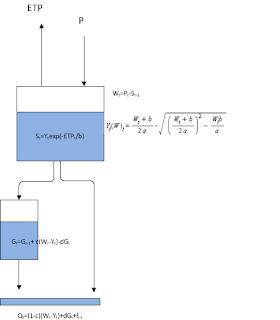
Figura 2: Esquema del modelo hidrológico conceptual de Schaake.
3.
Resultados
Se ha seleccionado
el periodo de enero 1964 a diciembre 1993 para la calibración y de enero 1994 a
diciembre 2002 para la validación. Con
el fin de utilizar los criterios de optimización se eligió la función objetiva
de Nash y Sutcliffe (1970).
Donde:
Qsi=
caudal simulado (m3/s).
Qob=
caudal observado (m3/s).
N= representa el
número de pasos de tiempo simulados.
Para evaluar la
bondad de los resultados del modelo durante los periodos de calibración y
validación, los intervalos se presentan el Cuadro 1. La eficiencia de Nash se
encuentra enmarcada como C3.
3.1
Optimización
del modelo Schaake
La optimización del
modelo fue realizada mediante técnicas de optimización global, donde un mínimo
global es un punto donde el valor de la función es menor que o igual al valor
en todos los otros puntos factibles.
Los valores
obtenidos para los parámetros del modelo Schaake fueron: Máximo déficit de
humedad en el reservorio del suelo Dmax=184.7435; parámetro que
representa la proporción de la actual evapotranspiración que debe ser
satisfecha por la precipitación en el mes actual antes de la escorrentía o la infiltración
que puede ocurrir Φ=0.3497; el parámetro que controla la infiltración de la
precipitación a través de la superficie del suelo z=0.0001; el parámetro del
modelo kk=0.1886; el valor umbral máximo para el modelo Gmax=184.9065.
En la figura 3 se muestra el comportamiento de los parámetros en el proceso de
optimización, en la figura 4 se muestra las variaciones de los parámetros
tomados de dos en dos de acuerdo al valor de Nash-Sutcliffe obtenido.
Figura 4:Variación de la eficiencia de la función Nash-Sutcliffe de acuerdo a la
variación de los parámetros Dmax, Φ ,z, kk, Gmax , superficies
generadas tomando de dos en dos los parámetros.
3.2
Calibración
del modelo Schaake
En el periodo de
calibración (1964-1993) el modelo Schaake presentó una eficiencia de Nash-Sutcliffe
de 90.95 % considerado como una calidad
excelente de acuerdo a la tabla 1. En la figura 5 se muestra los caudales
simulados comparados con los observados.
Figura 5: Caudales observados y simulados por el modelo Schaake en la cuenca del
río Lurín
(Periodo de
calibración)
3.3
Validación
del modelo Schaake
Figura 6:Caudales observados y simulados por el modelo Schaake en la cuenca del
río Lurín
(Periodo de
validación).
4.
Conclusión
- De acuerdo a los resultados obtenidos, el modelo Schaake se presenta como adecuado para la simulación hidrológica en la cuenca del río Lurín, presenta una eficiencia de 90.95 % y 93.04 % para los periodos de calibración y validación respectivamente.
5.
Referencias
bibliográficas
- Fernandez, R; Vogel, S. 2000. Regional calibration of watershed model. Hydrological Sciences-journal-des-Sciences Hydrologiques, 45(5): 689-707.
- Jiang, T; Xu, C. 2007. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. Journal of Hydrology 336: 316-333.
- Miroslaw, D; Okruszko, T. 2011. Modelling of Hydrological Processes in the Narew Catchment. New York, US.Springer. 153 p.
- Schaake, J.C., 1990. From climate to flow. In: Waggoner, P.E. (Ed.), Climate change and US Water Resources. John Wiley & Sons, New York, pp. 177–206.
- Schaake, J.C., Liu, L.Z., 1989. Development and application of simple water balance models to understand the relationship between climate and water resources. In: Kavvas, M.L. (Ed.), New Directions for Surface Water Modelling (Proceedings of the Baltimore Symposium, May 1989). IAHS Publication, No.181, pp. 345–352.
Aplicación en MATLAB