APLICACIÓN EN MATLAB PARA EL CÁLCULO DE LA INFILTRACIÓN
La infiltración del agua en el suelo y su movimiento en la zona no saturada del mismo es de fundamental importancia en la actividad agropecuaria. El proceso de infiltración influye en el intercambio de agua entre el sustrato y las plantas y se ve afectado por las labores realizadas en el suelo (Narro Faría, 1994). La infiltración, como una componente del ciclo hidrológico, está relacionada con el escurrimiento superficial que puede producir erosión y con la recarga de los acuíferos y su vulnerabilidad a la contaminación. Por lo tanto, es de suma importancia su evaluación para un manejo sustentable de las tierras que procure evitar su degradación. La determinación de los parámetros hidráulicos en la zona no saturada, tales como la sortividad y la conductividad hidráulica constituye el primer paso para poder utilizar modelos hidrológicos que puedan predecir el movimiento del agua.
Ecuación de Smith-Parlange (1978)
La ecuación de Smith-Parlange, desarrollada por Woolhiser en 1989, es la siguiente:
Donde:
F : Infiltración acumulada [L]
f : Velocidad de infiltración [L/T]
Ks : Conductividad hidráulica a saturación natural [L/T]
B = G (θs - θ1 )
o B = G φ (S max - S1)
θ s : Contenido de humedad a saturación natural (L3 /L3)
θ1 : Contenido de humedad inicial ((L3 /L3)
φ : Porosidad del suelo [L3 /L3]
S : Saturación relativa
Smáx : Saturación relativa máxima
S1 : Saturación relativa inicial
y G es definida como:
En la cual:
h: potencial de presión [L]
K(h) : Conductividad hidráulica [L/T]
G : Potencial de escurrimiento o potencial de presión debido a capilaridad [L]
Por otro lado, se tiene que:
Con lo cual, utilizando la ecuación de Averyanov (1949) citado por Poluvarinova-Kochina
(1962).
Y la ecuación de van-Genuchten (1980):
Donde:
η, m, n y hg son parámetros empíricos
h : potencial de presión [L]
Se puede llegar a:
Cálculo de la lámina infiltrada hasta el inicio del encharcamiento
Dada una intensidad de lluvia en el momento en que se realiza el cálculo de la infiltración, se calcula en primer lugar la lámina que se acumulará hasta el inicio del encharcamiento (bajo el supuesto de que no cambia la intensidad de precipitación). Esta lámina acumulada se determina a partir de la primera ecuación. Como se conoce la intensidad media de lluvia se puede considerar que:
Donde ip es la intensidad media de precipitación que se tiene al alcanzar el valor de F. Despejando F de esta ecuación se llega a:
Cálculo del Tiempo de Encharcamiento
Una vez que se conoce F se procede a determinar el tiempo que se tarda en llegar al encharcamiento, para lo cual se integra la ecuación:
Donde t1 es el tiempo de encharcamiento y F1 es el valor calculado a partir de Ks e Ip.
Calculo de la lámina infiltrada después del encharcamiento
Una vez que se conoce el valor del tiempo de encharcamiento (t1) se puede determinar el valor de la lámina que se infiltra después de que se ha llegado al encharcamiento.
Para calcular el valor de 'F', se utiliza la ecuación del tiempo de encharcamiento con 'F' en lugar de 'F1' y 't' en lugar de 't1' y se aplica el método de Newton-Raphson.
En el cálculo de la infiltración se debe elegir correctamente el primer estimador de F para que haya convergencia al utilizar el Newton-Raphson; un buen estimador es:
El valor de 'F' se va aproximando cada vez más según: Donde 'j' denota el paso de tiempo y 'k' la iteración respectiva y
Se conseguirá la solución cuando:
Aplicación
Resultados:
Video:
Parlange
Cargado por eber23. - Videos de los últimos descubrimientos en ciencia y tecnología.


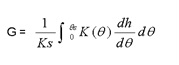













Amigo, muy buen trabajo, pero podrias compartir la aplicación que realizaste, sería muy útil para quienes aprendemos la materia.
ResponderEliminarMuchas Gracias
Hola Albert, aquí esta el link:
ResponderEliminarhttps://www.dropbox.com/s/mjoz4i0bqy5em8p/Parlange_pkg.rar
un favo link caido
ResponderEliminarun favor lo podrias resubir, link caido, muchas gracias
ResponderEliminar